What is a binary search tree?
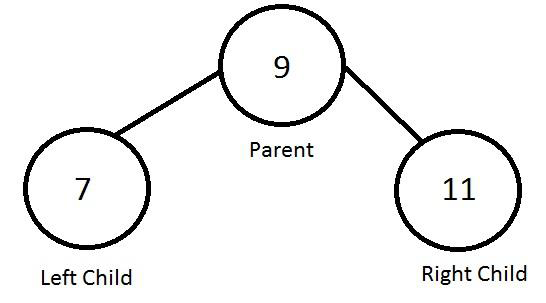
A binary search tree is a data structure organized in a hierarchical structure of notes which is used for searching. Likewise, Its purpose is for storing data for rapid access, storage, and deletion. Data in a search tree are stored in the tree nodes, which must have associated with them a value or key.
Similarly, the keys are used to structure the tree so that the value of the left child node is less than that of the parent node and the value of the right child node is greater than that of the parent node. Typical key storage values include strings, integers, and doubles.
Basic operations of a binary search tree
Insertion
Adding a value to a search tree can be broken down into two stages
- Searching for a place to insert the new element
- Inserting the new element into this place
The steps of insertion of a binary search tree
1. Check to see if the value in the current node and a new value are equal. If so, a duplicate is found.
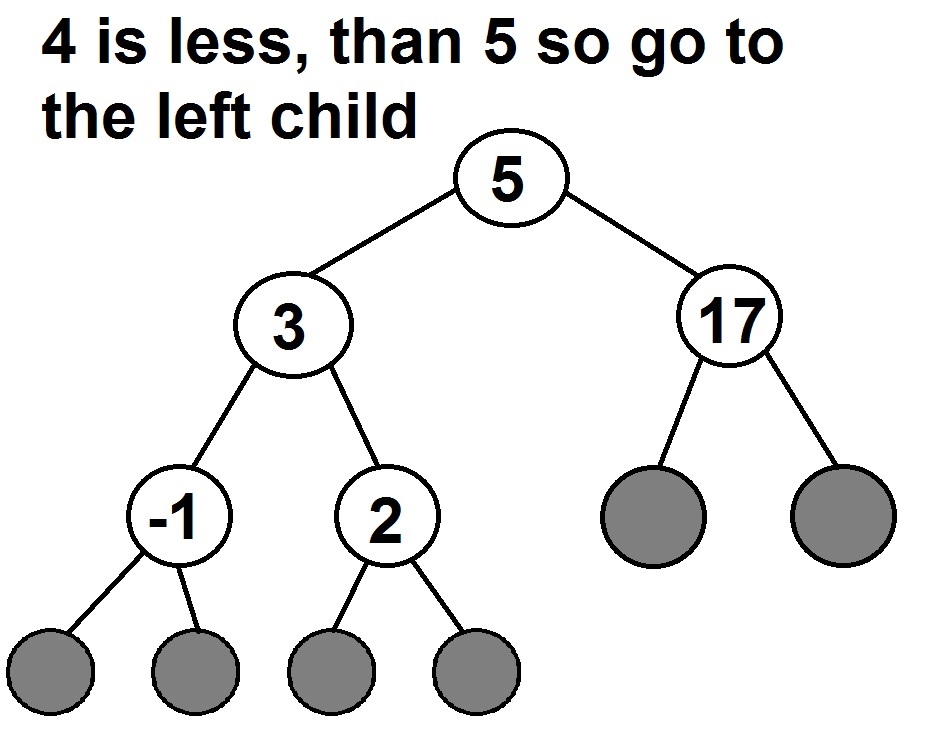
2. If a new value is less than the node’s value:
- If the current node has no left child, a place for insertion has been found
- If not, handle the left child with the same algorithm
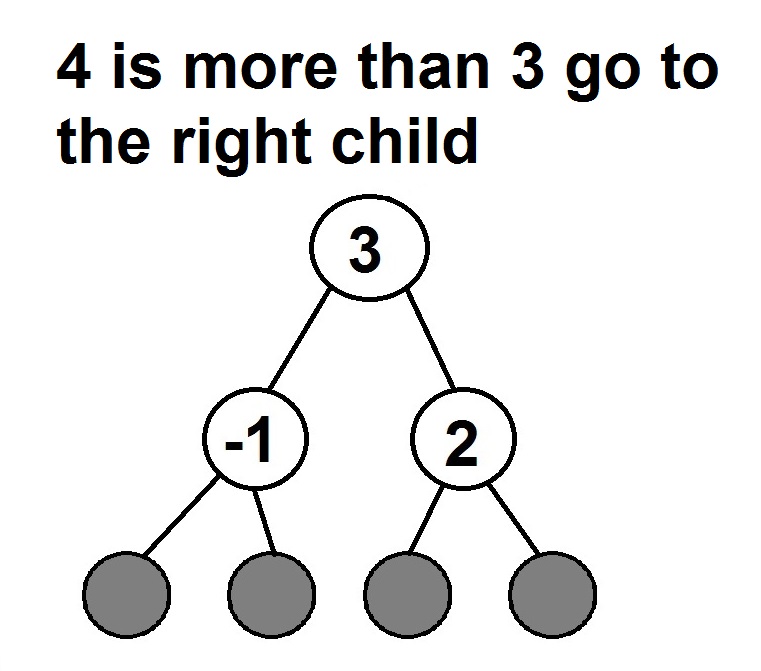
3. If a new value is greater than the node’s value:
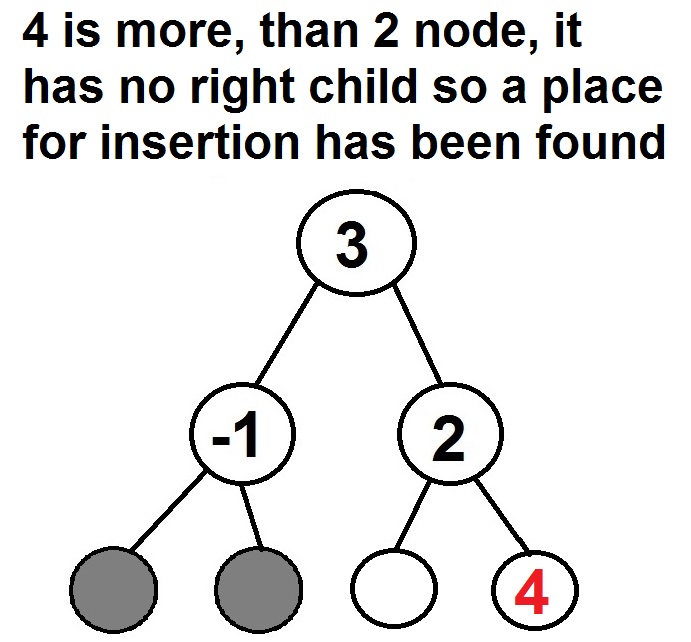
- If the current node has no right child, a place for insertion has been found
- If not, handle the right child with the same algorithm
Example – Insert 4 to the search tree
The insertion code sample in C++
</pre>
<pre>// Insertation code example
bool BinarySearchTree::add(int val)
{
if(root == NULL)
{
root = new BSTNode(val);
return true;
}
else
return root−>add(val);
}
bool BSTNode::add(int val)
{
if(val == this−>value)
return false;
else if(val < this−>value)
{
if(left == NULL)
{
left = new BSTNode(val);
return true;
}
else
return left−>add(val);
}
else if(val > this−>value)
{
if(right == NULL)
{
right = new BSTNode(val);
return true;
}
else
return right−>add(val);
}
return false;
}
</pre>
<pre>
Searching
Searching for a value in a search tree is similar to an insertion operation. The search algorithm traverses the tree in detail, so a proper choice can be made.
The steps of searching a binary tree are:
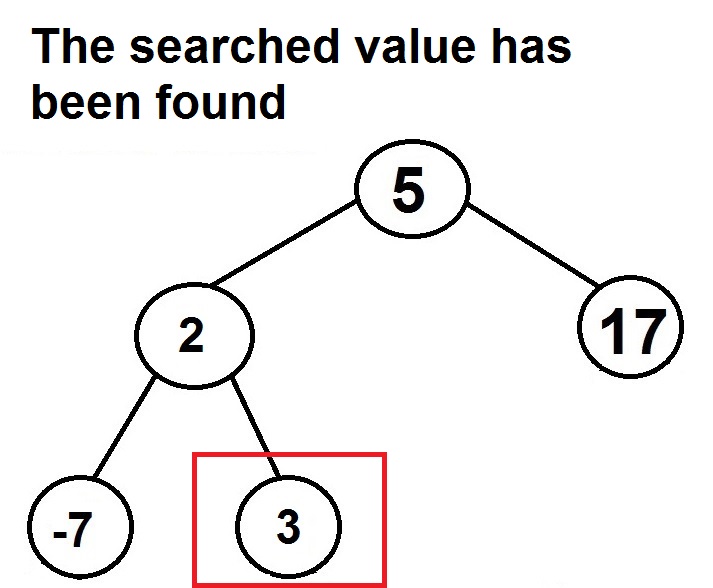
1. Check the value in the current node and searched value are equal. If so, the value is found. Otherwise
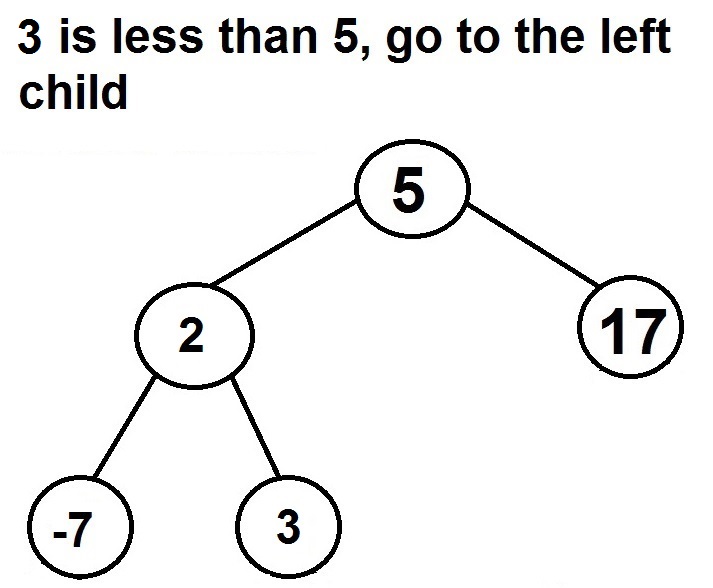
2. If the searched value is less than the node’s value
- If the current node has no left child, the searched value doesn’t exist in the binary search tree
- If not, handle the left child with the same steps
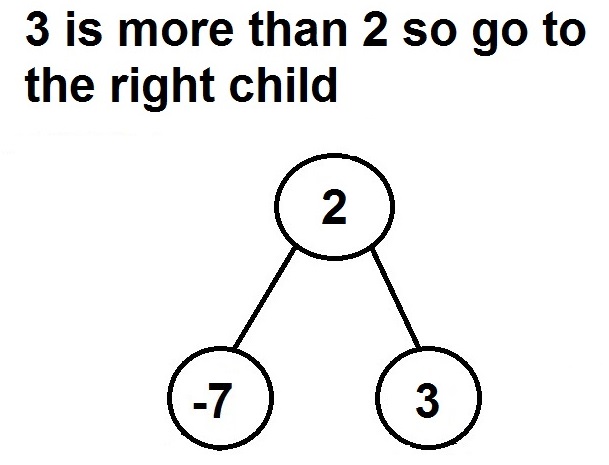
3. If a new value is greater than the node’s value
- If the current node has no right child, the searched value doesn’t exist in the binary search tree
- If not, handle the right child with the same steps
Example – Search for 3 in the binary search tree
Searching C++ code sample
// Searching code example
bool BinarySearchTree::search(int val)
{
if(root == NULL)
return false;
else
return root−>search(val);
}
bool BinarySearchTreeNode::search(int val)
{
if(value == this−>val)
return true;
else if(val < this−>val)
{
if(left == NULL)
return false;
else
return left−>search(val);
}
else if(val > this−>value)
{
if(right == NULL)
return false;
else
return right−>search(val);
}
return false;
}
Deletion
The operation of deletion is more complex than add and search. It can be broken down into two parts
- Searching for a node to remove
- If the node is found, run the remove steps
There are three concepts of deletion which are:
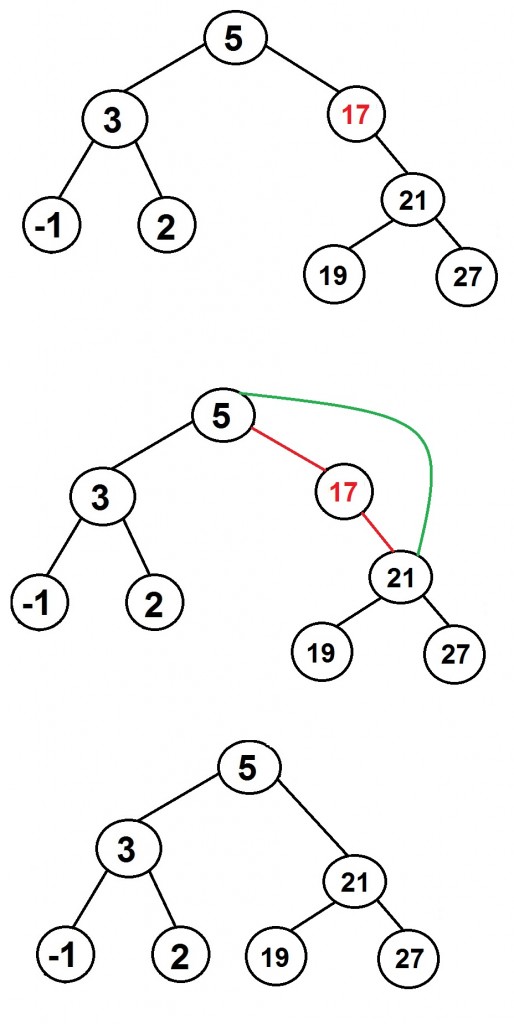
1. Node to be removed that has one child
The node is cut from the search tree and the algorithm links the single child with its subtree directly to the parent of the removed node.
Example: Remove 17 from the binary search tree
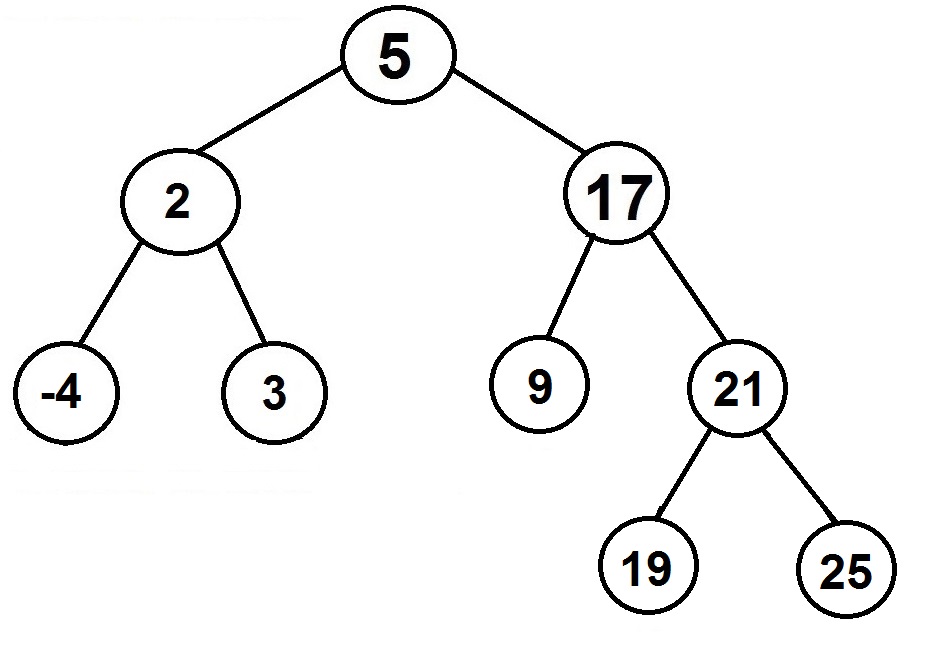
2. Node to be removed that has two children
The steps are
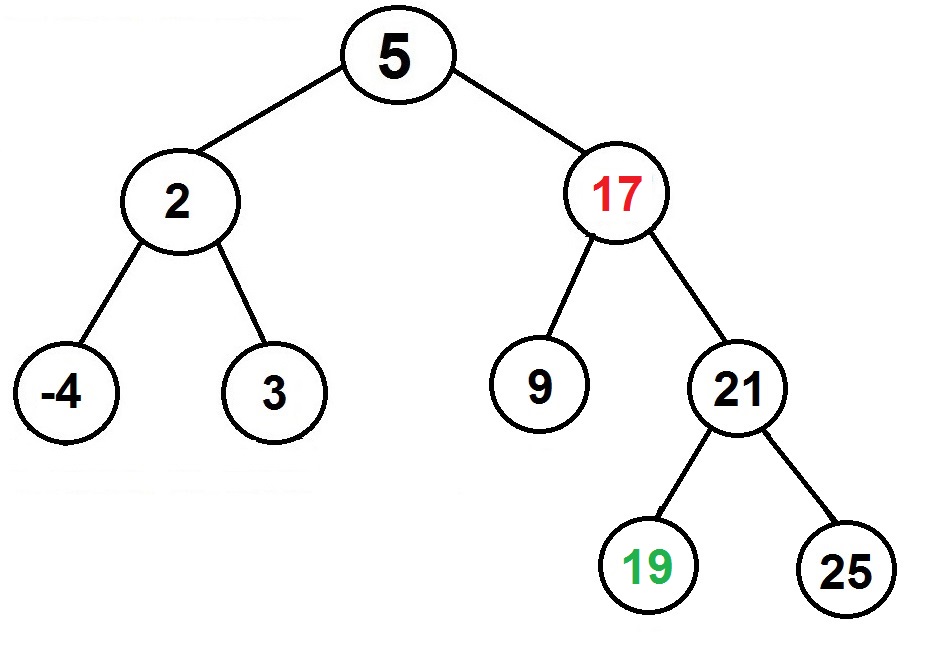
– Find the minimum value in the right subtree
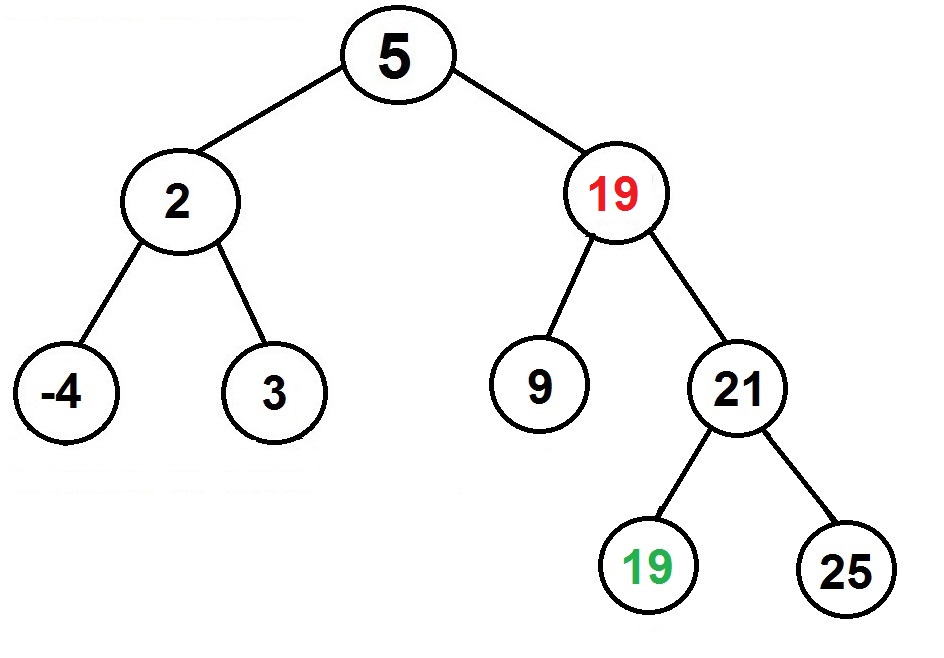
– Replace the value of the node to be removed with the minimum value found in the previous step
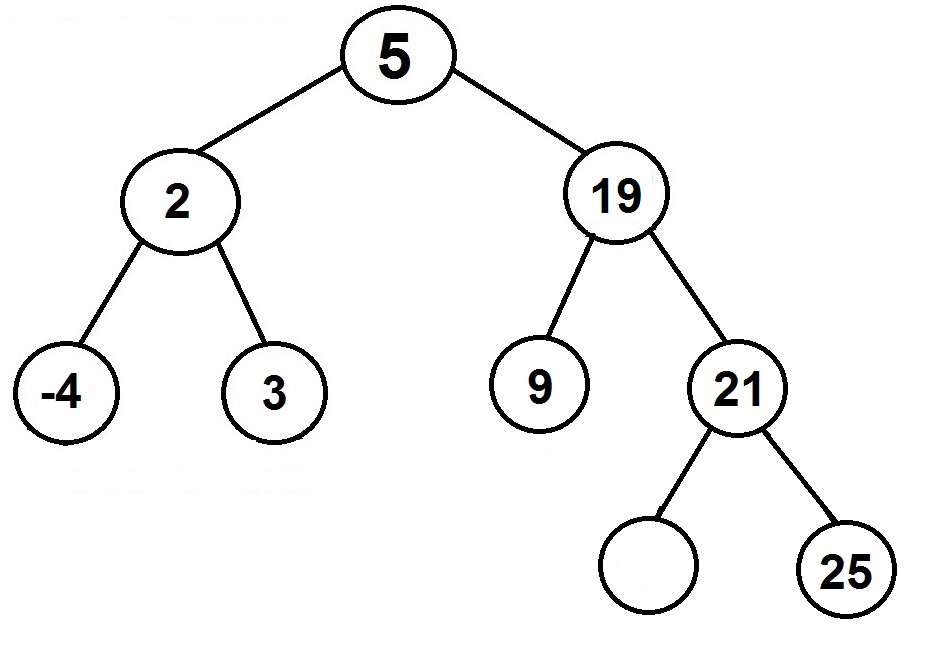
– Call the removing step to the right subtree to remove a duplicate
Example: Remove 17 from the binary search tree
3. Node to be removed that has no children
This case is the easiest. The algorithm sets a corresponding link of the parent to NULL and disposes of the node.
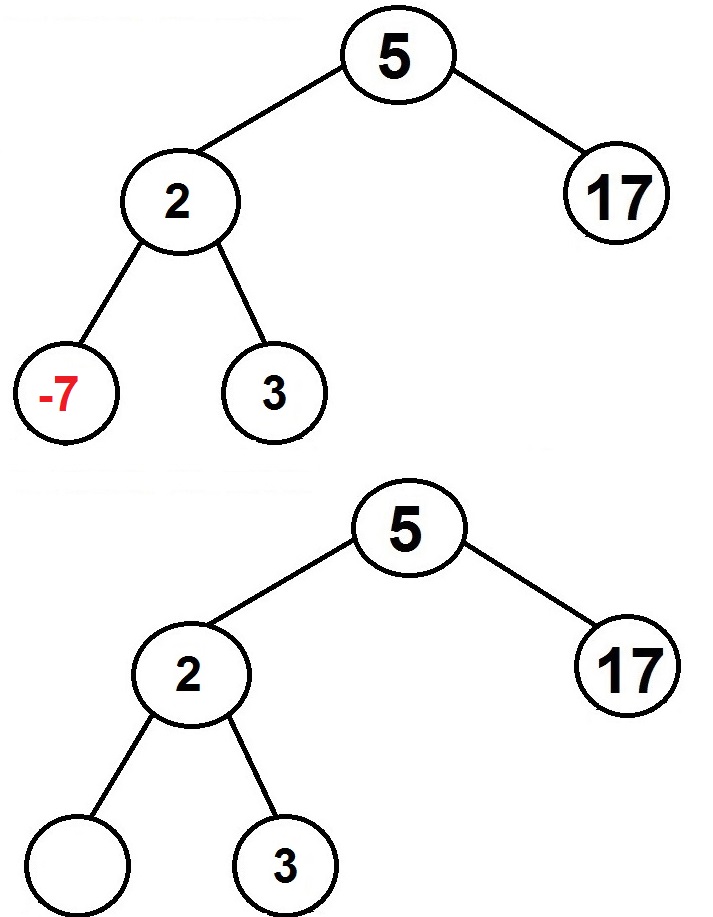
Example – Remove -7 from the binary search tree
</pre>
<pre>// Deletion
bool BinarySearchTree::remove(int val)
{
if(root == NULL)
{
return false;
}
else
{
if(root−>getValue() == val)
{
BinarySearchTree_Node auxRoot(0);
auxRoot.setLeftChild(root);
BinarySearchTree_Node* removeNode = root−>remove(val, &auxRoot);
root = auxRoot.getLeft();
if(removeNode != NULL)
{
delete removeNode;
return true;
}
else
{
return false;
}
}
else
{
BinarySearchTree_Node removeNode = root−>remove(value, NULL);
if(removeNode != NULL)
{
delete removeNode;
return true;
}
else
return false;
}
}
}
BinarySearchTree_Node* BinarySearchTree_Node::remove(int value, BinarySearchTree_Node *parent)
{
if(value < this−>val)
{
if(left != NULL)
return left−>remove(val, this);
else
return NULL;
}
else if(value > this−>val)
{
if(right != NULL)
return right−>remove(val, this);
else
return NULL;
}
else
{
if(left != NULL && right != NULL)
{
this−>val = right−>minVal();
return right−>remove(this−>val, this);
}
else if(parent−>left == this)
{
parent−>left = (left != NULL) ? left : right;
return this;
}
else if(parent−>right == this)
{
parent−>right = (left != NULL) ? left :right;
return this;
}
}
}
int BinarySearchTree_Node::minVal()
{
if(left == NULL)
return val;
else
return left−>minVal;
}</pre>
<pre>